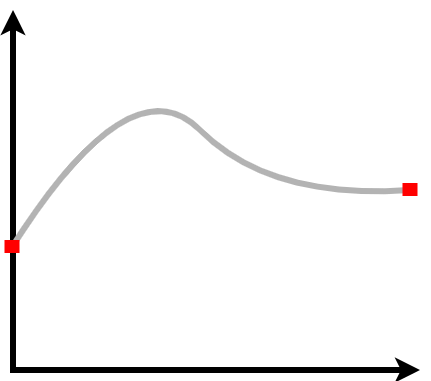
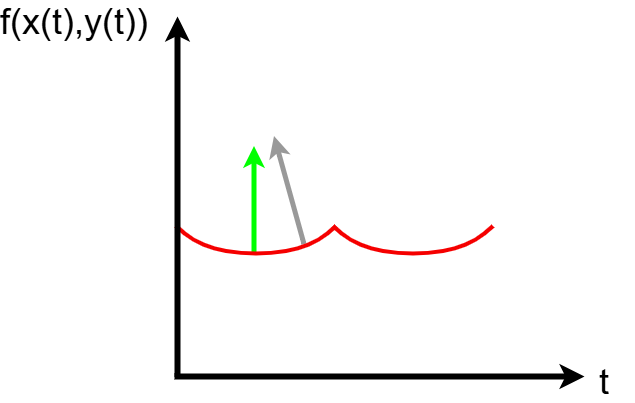
boundary of f(x, y)
We are searching for global extrema in f(x, y), over the bounded region.
g(x, y) = k
The inputs (x, y) are limited to this region. Thus, this indicates the domain over which we are finding the global extrema.
next step...
How do we check for global extrema over this domain?
Step 2: Parallel Between R2 and R3
to find global extrema in R2
You need to check points where:
- the derivative of f is zero (interior points)
- the endpoints of f (boundary points)
generalization
If you’re looking for the local extrema, you can exclude the boundary. However, since you’re looking for global extrema, you must include the boundary.
to find global extrema in R3
Thus, you need to check points where:
- the gradient of f is zero (interior points)
- boundary curve
However, it may be difficult to find a closed form of the boundary curve, and it may also be difficult to parameterize it.
Method 2 for Finding Extrema on Boundary Curve
Step 4: Using normal vectors
@ extrema
Notice that, in the projected boundary in R2, a horizontal tangent vector is synonymous with a vertical normal vector.
@ non-extrema
Notice that, at non-extrema in R2, the normal vector is not vertical.
transfer to R3
We could find t and then find the critical point
(x(t), y(t), f(x(t), y(t))), as in Method 1. However, to avoid parameterizing the boundary, let's use a trick.
Step 5: Using gradient vectors
@ extrema
Notice that, from the top view in R3, the gradient vector at a global minimum is parallel to the normal vector of g(x,y) = k.
@ non-extrema
Conversely, the gradient vector at non-extrema is not parallel (from the top view) to the normal vector of g(x,y) = k at that same (x, y).
generalization
Thus, we are looking to find points (x, y) where the gradient vector of f and the normal of g = k are parallel.
We can see that this is true using the example of the critical and non-critical point above:
- At the minimum, moving along the boundary in any direction will increase f. Thus, moving perpendicular to the boundary is the direction of steepest descent (the gradient).
- At the non-critical point, moving leftward along the boundary will decrease f. Thus, the direction of steepest descent (the gradient) is not perpendicular to the boundary.